一級建築士試験　令和3年度　学科Ⅳ（構造）№02

こんばんは、

現在の時刻2023年04月19日20時45分

建築士試験まで、後95日。

さぁ、

迫って参りました。

構造は、

図からの問題が多いですね。

昨日の復習に他年度の同系問題を探そうと思ったのですが、

平成29年度まで戻るので、とりあえずそのまま令和3年を続けることにしました。

では、

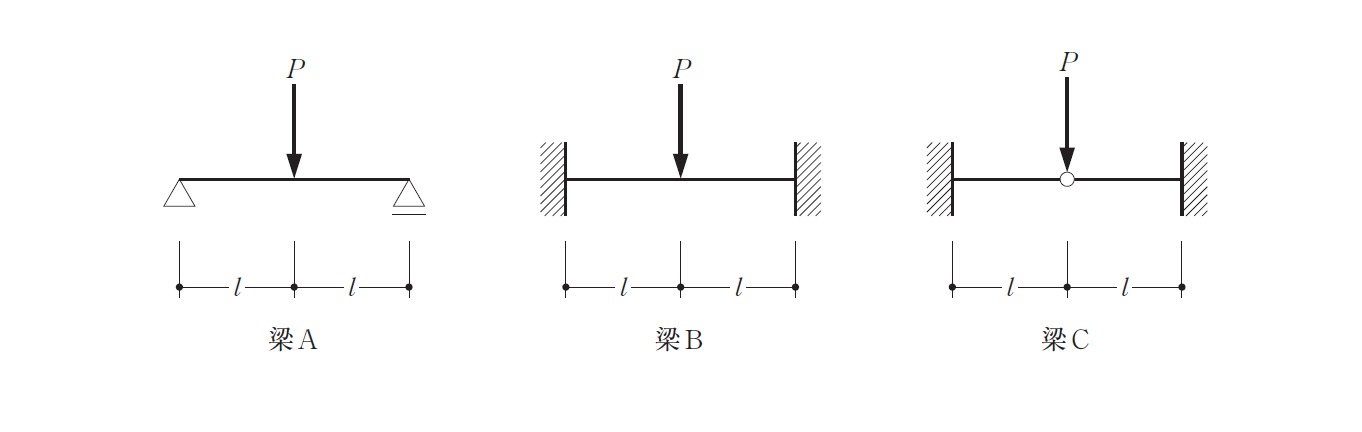
〔Ｎｏ． 2 〕図のような梁Ａ、梁Ｂ及び梁Ｃにそれぞれ荷重P が作用している場合、梁Ａ、梁Ｂ及び梁Ｃにおける応力、たわみ等の大きさの比（梁Ａ：梁Ｂ：梁Ｃ）として、最も不適当なものは、次のうちどれか。ただし、全ての梁は同一断面で、全長にわたって等質等断面の弾性部材とし、自重は無視する。

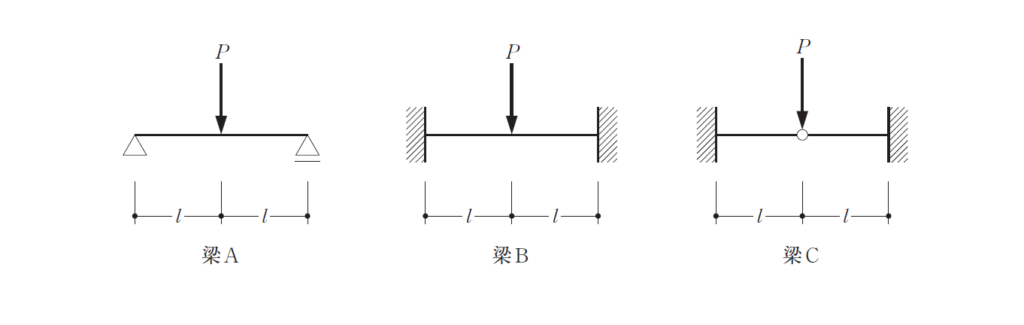
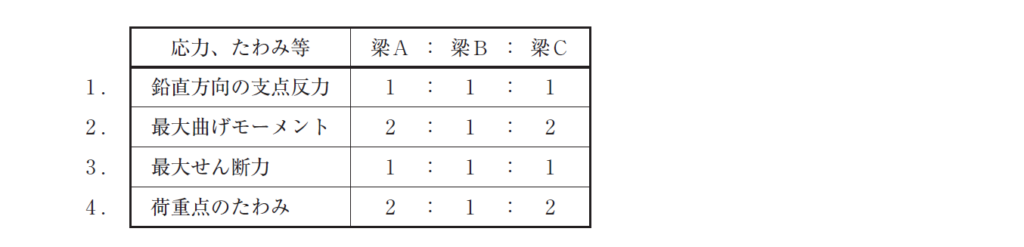
１．支点の反力は、P/2で、全て同じのはずなので　正しい。

２．曲げモーメントは、梁A（Pℓ/2）：梁B（Pℓ/4）：梁C（Pℓ/2）＝1/2：1/4：1/2＝２：１：２　

３．せん断力は、P/2で全て同じですよね。

４．たわみの公式からです。梁A＝８Pℓ/48EI：梁B＝8Pℓ/192EI：梁B＝Pℓ/6EI　　

　　　梁A=Pℓ/6：梁B＝Pℓ/14：梁C＝Pℓ/6

これでいうと

正解は4番ですね。

で、正答は、

4番です。

公式を調べながらになりますが

とりあえずOKです。

ちなみに、

平成29年の問題ですが、

　　

〔N o．１〕図－１のように、脚部で固定された柱の頂部に鉛直荷重􌐲及び水平荷重􌑎が
作用している。柱の断面形状は図－２に示すような長方形断面であり、鉛直荷重􌐲及び水
平荷重􌑎は断面の図心に作用しているものとする。柱脚部断面における引張縁応力度と圧
縮縁応力度との組合せとして、正しいものは、次のうちどれか。ただし、柱は等質等断面
とし、自重は無視する。また、応力度は弾性範囲内にあるものとし、引張応力度を􌓕＋」、
圧縮応力度を􌓕－」とする。

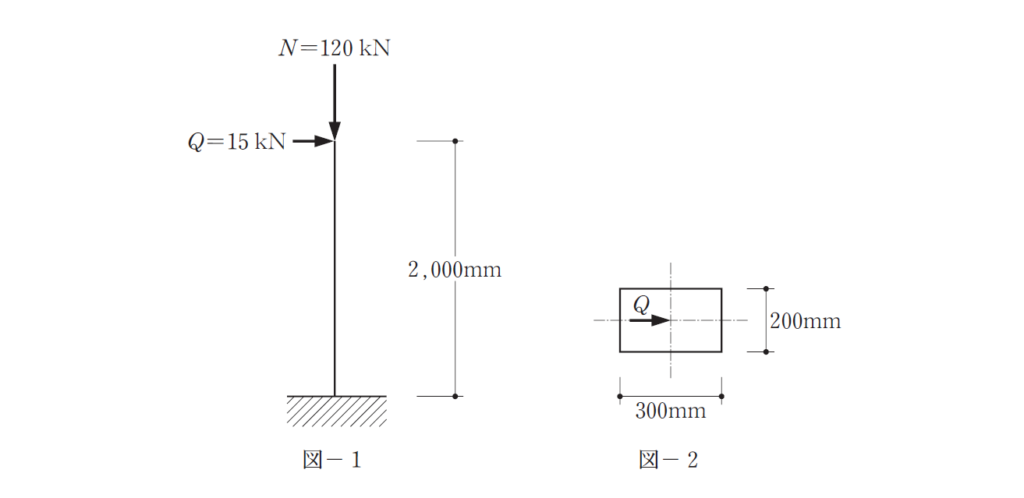
まずは、

引張応力度を計算すれば答えが出ますよね。

軸方向力　120/60　=　２

曲げモーメント　15×2000　=　30

断面積は60000

断面係数は、200×300×300/6　=3　

‐120/60＋30/3=‐2＋10=∔8

で、

引張縁応力度は、2番が正しいです。

で、正答は、

　　2番です。

まだ、

ふわっと覚えている感じですね。

法規もそうでしたけど、

少しづつでも頭に入れていきます。

では、